Rechenbeispiel 1: Rechtsseitiger Test
Eine Kleinstadt will ein neues Kulturzentrum erbauen.
Der Bürgermeister geht davon aus, dass höchstens 50% der Einwohner dem Vorhaben zustimmen.
Einige Kunst- und Kulturexperten vermuten dagegen, dass die Zustimmungsrate höher ist.
Bei einer Umfrage unter 200 Personen befürworten 120 Personen den Bau des Kulturzentrums.
Kann man nun bei einer Irrtumswahrscheinlichkeit von 4% davon ausgehen,
dass die Annahme des Bürgermeisters korrekt ist?
Lösung
Da man bei der Stichprobe nur zwischen „Treffer” (=Zustimmung) oder „kein Treffer”
(= Ablehnung) unterscheidet, handelt es sich um ein Zufallsexperiment mit Binomialverteilung.
Der Umfang der Stichprobe ist n=200.
- Was ist nun die Nullhypothese?
Üblicherweise verwendet man das, was geprüft werden soll als Nullhypothese. Da der
Bürgermeister eine Trefferwahrscheinlichkeit von p≤0,5 vermutet, ist H0 mit p≤0,5 die Nullhypothese
und die Alternative ist H1 mit p>0,5.
- Welche Art von Test liegt vor?
Die Zufallsvariable X, welche die Anzahl der Treffer beschreibt, ist gemäß H0 B(200;0,5)-verteilt.
Wenn sich nun herausstellt, dass die Anzahl der Treffer k höher ist als erwartet, so wird H0
zugunsten von H1 abgelehnt. Es handelt sich demnach um einen rechtsseitigen Test und es muss ein
Ablehnungsbereich der Form A=[k,...,200] gefunden werden.
Mit Hilfe der Irrtumswahrscheinlichkeit lässt sich k bestimmen.
Damit H0 abgelehnt wird, muss P(X≥k)<0,04 gelten.
Da der GTR den Ausdruck P(X≥k) nicht direkt berechnen kann, müssen wir diesen „GTR-gerecht” umformen.
Es gilt P(X≥k)=1-P(X≤k-1).
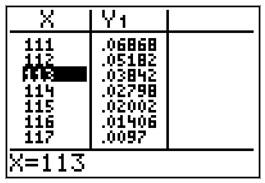
Somit gibt man im Y-Editor den Ausdruck 1-binomcdf(200,0.5,X-1) und sucht sich über 2ND TABLE den Wert von X,
beim dem dieser Ausdruck erstmals <0,04 wird.
Für X=112 stellt man α=0,05182 fest und X=113 liefert α=0,03842.
Somit ist X=113 der gesuchte Wert und das Ablehnungsintervall lautet A=[113,...,200].
Da bei der Stichprobe eine Trefferzahl T von 120 (d.h. 120 Zustimmungen) festgestellt wurden und T∈A ist,
wird H0 abgelehnt.
Ergebnis:
Die Kunst- und Kulturexperten haben bei einer Irrtumswahrscheinlichkeit von 4% Recht (d.h. H1 gilt)
und die Zustimmungsrate für das Kulturzentrum liegt über 50%.
Rechenbeispiel 2: Linkssseitiger Test
In einem Supermarkt hatte das Fertiggericht „Maxi Lunch” bisher einen Marktanteil von höchstens 30%.
Nach einer Untersuchung von Stiftung Warentest erhielt „Maxi Lunch” die Note 1.
Eine Woche nach dem Testbericht stellt der Marktleiter fest, dass von 240 Käufern von Fertiggerichten 60 „Maxi Lunch” gekauft haben.
Kann man bei einer Irrtumswahrscheinlichkeit von 10% davon ausgehen, dass der Marktanteil von „Maxi Lunch” gestiegen ist?
Lösung
Hier bedeutet „Treffer” = „gekauft” und „kein Treffer” = „nicht gekauft”.
Der Umfang der Stichprobe ist n=240.
- Was ist nun die Nullhypothese?
Üblicherweise, nimmt man das, was geprüft werden soll, bzw. das was behauptet wird als Nullhypothese. Folglich ist H0 mit p>0,3 (also die Annahme, dass der Marktanteil gestiegen ist und nun über 30% liegt) unsere Nullhypothese. Die Alternative ist H1 mit p≤0,3.
- Um welche Art von Test handelt es sich?
Die Zufallsvariable X, welche die Anzahl der Käufer beschreibt, ist gemäß H0 B(240;0,3)-verteilt.
Wenn sich nun herausstellt, dass die Anzahl der Käufer T kleiner ist als erwartet, so wird H0 zugunsten von H1 abgelehnt, was bedeutet, dass der Marktanteil nach wie vor höchstens 30% beträgt.
Es handelt sich somit um einen linksseitigen Test und es muss ein Ablehnungsbereich der Form A=[0,...,k] gefunden werden.
Es gibt eine kleine Eselsbrücke, mit der man etwas einfacher herausfinden kann, um welche Art Test es sich handelt. Die Art des Tests lässt sich nämlich direkt an der Gegenhypothese H1 ablesen.
Steht dort p≤... oder p<..., so handelt es sich um einen linksseitigen Test.
Haben wir p≥... oder p>..., so liegt ein rechtsseitiger Test vor.
Mit Hilfe der Irrtumswahrscheinlichkeit lässt sich k bestimmen.
Damit H0 abgelehnt wird, muss P(X≤k)<0,1 gelten. Man gibt im Y-Editor den Ausdruck binomcdf(240,0.3,X) ein und sucht sich über 2ND TABLE den Wert von X, beim dem dieser Ausdruck erstmals <0,1 wird.
Für X=62 stellt man α=0,08909 und für X=63 stellt man α=0,11471 fest. Somit ist k=62 der gesuchte Wert für das Ablehnungsintervall, das nunmehr die Gestalt A=[0,..,62] hat.
Da bei der Stichprobe die Trefferzahl T=60 (Käufer) festgestellt wurde und T∈A ist, wird H0 abgelehnt.
Ergebnis:
Der Marktanteil von „Maxi Lunch” liegt nach dem Testbericht von Stiftung Warentest mit einer Irrtumswahrscheinlichkeit von 10% nach wie vor bei höchstens 30%.
Rechenbeispiel 3
Leo ist Mitglied eines Schützenvereins und hat eine Trefferquote von höchstens 70%.
Nach einem mentalen Training nimmt Leo an, dass sich seine Trefferquote verbessert hat und testet dies auf dem Schießstand mit 100 Schuss.
Wie viele Treffer muss Leo mindestens erzielen, damit man mit einer Irrtumswahrscheinlichkeit von höchstens 5% davon ausgehen kann, dass sich seine Trefferquote wirklich verbessert hat?
Lösung
Der Umfang der Stichprobe ist n=100.
Wir nehmen wieder das, was wir prüfen wollen als Nullhypothese, d.h. H0 p>0,7.H1 mit p≤0,7 ist die Gegenhypothese, d.h. wir haben einen linksseitigen Test und das Ablehnungsintervall hat die Gestalt A=[0,...,k].
Für „Ablehnung” muss P(X≤k)≤0,05 gelten.
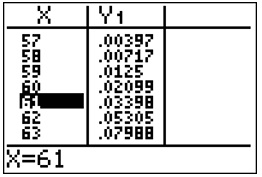
Im GTR gibt man den Ausdruck binomcdf(100,0.7,X) ein und prüft über 2ND TABLE, wann dieser Wert erstmals 0,05 unterschreitet.
Für X=62 erhält man noch &lapha;=0,05305 und X=61 liefert α=0,03398.
Somit ist k=61 der gesuchte Wert für das Ablehnungsintervall und wir haben A=[0,...,61].
Ergebnis:
Leo muss mindestens 62 Treffer erzielen, damit man bei einer Irrtumswahrscheinlichkeit von 5% davon ausgehen kann, dass sich seine Trefferquote verbessert hat.
Rechenbeispiel 4
Ein Hersteller von Speicherchips gibt an, dass erfahrungsgemäß höchstens 7% der Chips fehlerhaft sind.
Nach einer baulichen Änderung in den Produktionsräumen des Herstellers vermutet ein Kunde, dass sich die Fehlerrate vergrößert hat.
Der Kunde und der Hersteller vereinbaren einen Test, bei dem 210 Chips geprüft werden.
Die Nullhypothese H0 mit p≤0,07 wird abgelehnt, wenn dabei mehr als 23 Chips fehlerhaft sind.
Mit welcher Wahrscheinlichkeit irrt man sich und lehnt somit H0 zu unrecht ab?
Lösung
Wir haben n=210 und H0 mit p≤0,07. H1 besagt p>0,07.
Die Zufallsvariable X, ist gemäß H0 B(210;0,07)-verteilt.
Das Ablehnungsintervall ist mit A=[24,...,210] vorgegeben.
Die Irrtumswahrscheinlichkeit ist gegeben durch P(X≥24)=1-P(X≤23).
Über die Eingabe von 1-binomcdf(210,0.07,23) im GTR erhält man α≈0,0126.
Ergebnis:
Wenn man mehr als 23 fehlerhafte Chips in der Stichprobe findet und daher H0 vereinbarungsgenmäß ablehnt, so irrt man sich mit einer Wahrscheinlichkeit von höchstens 1,26%.
| Downloads |
PowerPoint